A complexidade de algoritmos e a notação Big-O são coisas que escutamos na faculdade, mas muitas vezes o conceito não fica claro imediatamente. Nessa publicação, vou tentar simplificar o entendimento da notação Big-O, aplicada na definição de complexidade de algoritmos, utilizando exemplos de código que mostram como essa notação varia e como nosso código pode ser melhor compreendido, do ponto de vista de desempenho, quando dominamos esse conceito.
Definição
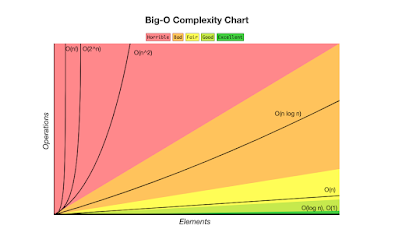
Em termos simples, a notação Big-O:- É relativa à complexidade de um algoritmo;
- Descreve como é o desempenho de um algoritmo e como ele escala;
- Descreve o limite superior da taxa de crescimento de uma função e pode ser entendido como o cenário de pior caso.
Um exemplo dessa notação: O(n²), temos que n é o número de elementos de uma função que recebe entradas. Assim, este exemplo nos diz que para n entradas, suas complexidade é igual a n².
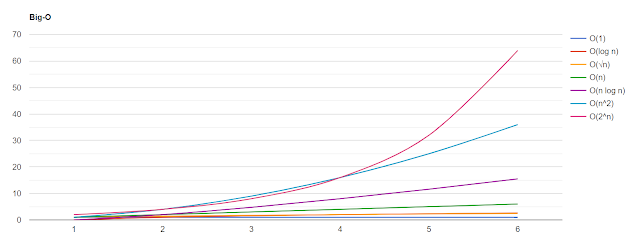
Desempenho das complexidades comuns
Exemplos em código
Alguns exemplos de código nos ajudam a clarear as coisas um pouco mais com relação a como a complexidade de uma função afeta o desempenho. Os códigos abaixo estão escritos em Python, mas, obviamente, poderiam estar escrito em outras linguagens.
O(1)
O(1) representa a função que sempre leva o mesmo tempo independente do tamanho da entrada.
O(n)
O(n) representa a complexidade de uma função que aumenta linearmente e em proporção direta ao número de entradas. Este é um bom exemplo de como a notação Big-O descreve o cenário de pior caso como uma função que pode retornar verdade após ler o primeiro elemento, ou falso após ler todos os n elementos.
O(n²)
O(n2) representa uma função cuja complexidade está diretamente proporcional ao quadrado do tamanho da entrada. Adicionar mais laços de iteração aninhados ao longo da entrada irá aumentar a complexidade, a qual pode ser representada por O(n³) com um total de 3 iterações e O(n⁴) com 4 iterações totais.
O(2ⁿ)
O(2ⁿ) representa uma função onde o tempo de computação dobra para todo elemento de entrada. O exemplo acima é o cálculo recursivo dos números de Fibonacci. A função se encaixa em O(2ⁿ) conforme a função recursivamente chama a si mesma duas vezes para cada número de entrada, até que o número seja menor ou igual a um.
O(log n)
O(log n) representa uma função cuja complexidade aumenta logaritmicamente conforme o tamanho da entrada aumenta. Isso torna a escalabilidade de funções O(log n) bem aceitável, já que lidar com grandes entradas fica menor propenso a causar problemas de desempenho. O exemplo acima utiliza busca binária para verificar se a lista de entrada contém um certo número. Em termos simples, ela dividde a lista em duas em cada iteração até que o número seja encontrado ou o último elemento seja lido. Este método possui a mesma funcionalidade do exemplo O(n) - apesar da implementação ser completamente diferente e mais difícil de compreender. Porém, ela é premiada com um desempenho muito melhor com entradas grandes.
O lado negativo deste tipo de implementação é que uma Busca Binária baseia-se em elementos que já estejam em uma ordem correta. Isso adiciona um pouco de sobrecarga no desempenho geral se os elementos precisarem ser colocados em ordem antes de serem percorridos.
Conclusão
Há ainda muito mais para discutir sobre a Notação Big, mas espero que você agora tenha uma ideia básica do que é Big-O, seu significado e como ele pode ser traduzido e aplicado no seu código.




0 Comentários